Discussion on Calculation Formula of Valve Seal Specific Pressure

 Discussion on Calculation Formula of Valve Seal Specific Pressure

1 Overview

The valve must have a specific pressure calculation formula to limit the three key sealing parameters, such as the elastic modulus of the metal sealing surface material, the change in the surface roughness of the sealing surface and the thickness of the sealing layer, which control the basic conditions of its sealing, to the constant term C and coefficient K of the calculation formula. In the method, the regulation of the sealing specific pressure is weakened, and the correcting force specific pressure for correcting the sealing plane is not included, which reduces the accuracy of judging the basic conditions of the sealing. The analysis shows that the sealing specific pressure composed of the sealing force specific pressure and the corrective force specific pressure can meet the basic requirements of valve sealing.

2 Sealing conditions

In addition to the difference in medium pressure or concentration on both sides of the seal, the gap between the sealing surfaces is the main way of leakage. For flat seals, the plane of the sealing surface should be corrected first with the help of corrective force to eliminate the distance between the two sealing surfaces due to the surface shape error, so that the sealing surfaces are in close contact and conform to the shape, and a continuous contact surface with sufficient width is obtained. Secondly, the sealing surface is squeezed with sealing force, and part of the surface wave crest is squeezed into the wave valley, so that the average arithmetic deviation of the surface profile is reduced from 0.2-0.4 μm to 0.1-0.3 μm, forming an effective closed sealing ring. The sealing specific pressure superimposed by the specific pressure of the sealing force and the specific pressure of the correction force is generated on the sealing surface, which compresses or even blocks the local leakage channel, extends and changes the direction of the channel, and creates the basic conditions for the labyrinth seal.

3 Necessary specific pressure

The commonly cited empirical calculation formula of necessary specific pressure is [1]

The process of squeezing the sealing surface is mainly the process of elastic deformation, so when the surface roughness meets the sealing requirements, the surface compressive stress of the sealing surface should be calculated according to Hooke's law (assuming the flatness error is 0). The sealing force ratio is

If the hardness difference between the two sealing surfaces in the sealing pair is large, the softer sealing surface may be squeezed alone. If the hardness of the material is similar, it is possible that the two sealing surfaces are staggered and squeezed against each other. Therefore, ΔL in formula (2) is calculated according to the compression amount of one-side sealing surface. It is impossible to completely fill the wave peaks into the wave valleys by extrusion, and the surface roughness after extrusion is only a conceptual value that is easy to calculate. The surface roughness ε of the sealing surface after extrusion is

3.1 Calculation formula

The calculation formula of the specific pressure must also conform to Hooke's law. Solve the calculation formula of Hooke's law. According to different materials, take two sets of technical parameters that can effectively achieve sealing, and solve the coefficients C and K related to the sealing surface material. Copy The formula for calculating the necessary specific pressure for the sealing surface of different materials is obtained.

(1) Steel and carbide sealing surfaces

Combined solution of Equation (1), Equation (2) and Equation (3), the calculation mode applicable to the metal sealing surface is

Taking the stainless steel sealing surface as an example, E=21×105 MPa, L=2 mm, a=04 μm, a set of data is DN300, PN=64 MPa, bm=9 mm, λ=24 8 %, and another set of data is DN100, PN=16 MPa, bm=45 mm, λ=181 %, respectively substituted into formula (5), and listed the equations about coefficients C and K

Solve the equation system to get C=35, K=10, substitute into formula (1), copy the necessary specific pressure calculation formula suitable for steel and cemented carbide sealing surface

By the joint solution of equation (3) and equation (4), we getε1=03 μm，ε2=033 μm。

(2) Copper alloy sealing surface

Taking HPb59-1 sealing surface as an example, E=1034×105 MPa, L=15 mm, a=04 μm, a set of data is PN=25 MPa, bm=5 mm, λ= 282 %, and another set of data is PN=10 MPa, bm=35 mm, λ=245 %, respectively substituted into equation (5), and listed the equations about the coefficients C and K

Solving the equations, C=30, K=10, and substituting into formula (1) to copy the necessary specific pressure calculation formula for copper alloy sealing surface

By the joint solution of formula (3) and formula (4), ε3=029 μm and ε4=03 μm, respectively.

(3) Rubber sealing surface

Stress and strain relationship according to Hooke's law

q=δE   　　　　　　　　　　 　　　　　　　　（8）

Taking the rubber sealing surface as an example, set L=2 mm, E=784 MPa, one set of data is PN=25 MPa, bm=15 mm, δ=20 %, and the other set of data is PN=15 0 MPa, bm=7 mm, δ=152 %, formulas (1) and (8) are solved together, and the calculation model for the rubber sealing surface is

Substitute the data into equation (7), and list the equation system about the coefficients C and K

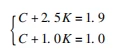
Solve the equations to get C=04, K=06, substitute into formula (1), copy the necessary specific pressure calculation formula suitable for the rubber sealing surface

3.2 Comparative analysis

The examples selected in the calculation process of the required specific pressure are the two intersection points of the specific pressure calculation formula and the expression of Hooke's law. Although the collection of the examples is accidental, they all meet the basic requirements of valve sealing. It can be seen that the specific pressure calculation formula must not be Hooke's law is not completely excluded, but due to their respective principles and curve trends, they have actually formed different scopes of application. Comparing Equation (1) with Equation (5) and Equation (9) respectively, it can be seen that the specific pressure calculation formula must limit the key parameters that control the sealing performance to the constant C and the coefficient K, and will adjust the function of the specific pressure of the seal. Only in relation to nominal pressure and sealing face width, which are not directly related to sealing performance, the direct regulation of key parameters of sealing performance is eliminated. In terms of sealing concept, there is a gap between the sealing principle of Hooke's law and the elastic deformation of the sealing layer. In the design principle, the key parameters of the sealing and the influence of the flatness of the sealing surface on the sealing performance are ignored.

4. Sealing force ratio

The sealing surface is elastically deformed after being squeezed by the sealing force, and its surface compressive stress is the specific pressure of the sealing force. Hooke's law can be used to deduce the calculation formula of the specific pressure of the sealing force for different materials. However, the deformation of metal materials is reflected in the change of the surface roughness of the sealing surface, which is in the order of micrometers, while the deformation of non-metallic materials is reflected in the compression of the sealing layer, which is in the order of millimeters. So the calculation mode is slightly different.

4.1 Calculation formula of sealing force specific pressure

(1) Metal seal

Combine Equation (2) and Equation (4), and sort out the sealing force specific pressure calculation formula for metal sealing

In formula (11), the specific pressure qm of the sealing force is proportional to the elastic modulus E of the metal sealing surface material and the surface roughness change (a-ε) before and after extrusion, and is inversely proportional to the thickness L of the sealing layer.

(2) Non-metallic seal

The sealing force specific pressure calculation formula for non-metallic sealing is calculated according to the expression of Hooke's law.

In formula (12), the specific pressure qm of the sealing force is proportional to the elastic modulus E of the material and the compression rate δ of the sealing layer.

4.2 Sealing parameters

The influence of sealing related parameters on the necessary specific pressure and the sealing force specific pressure was compared and analyzed.

(1) medium working pressure p

Taking H44H-150Lb DN50 as an example, take bm=45 mm, L=2 mm, DMN=51 mm. The actual specific pressure q=71 MPa is calculated, which is less than the required specific pressure qMF=82 MPa. This not only determines that the sealing surface cannot be sealed, but also cannot be sealed when it is lower than the nominal pressure. Field testing shows that the grinding roughness Ra of the sealing surface of the product is 02~04 μm, and the sealing is achieved by pressing the medium pressure, ε=015~03 μm.

(2) Width of sealing surface bm

The necessary specific pressure is defined as the minimum compressive stress that must be achieved in order to achieve sealing on the sealing surface, so the necessary specific pressure is always the same regardless of the width of the sealing surface. However, in the calculation formula (1) of the necessary specific pressure, when the width of the sealing surface increases, the calculated value of the necessary specific pressure decreases (Table 1), which is inconsistent with the definition. If analyzed according to Hooke's law, the width of the sealing surface has nothing to do with the specific pressure of the sealing force. Taking the J41T-25Q-DN150 valve as an example, take a=04 μm, ε=03 μm, L=2 mm, and the copper alloy sealing surface width bm is 7 mm and 35 mm respectively [1], [ 2]. After practical use, the valve can also effectively achieve long-term sealing when bm=35 mm.

Table 1. The width of the sealing surface and the required specific pressure

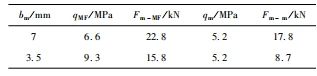
In the daily assembly test process, it is often seen that the indentation on the surface of the sealing surface does not reach the design width, that is, the fit is less than 65%, but it does not affect the completion of the sealing performance test. Taking the H41W-16T-DN32 valve as an example, the sealing surface of the valve body is a spherical section line seal, the spherical radius is r=1 mm, L=15 mm, and the surface roughness is Ra06~10 μm. 100 %, and when the low medium pressure is 10 MPa or 05 MPa, the sampling pass rate is 90 %. It can be seen that the width of the sealing surface is not directly related to whether it can be sealed, but is related to the mechanical strength (deformation, impact) and service life (wear, corrosion) of the sealing layer.

Practice has shown that a wider sealing surface is beneficial to extend the leakage channel, increase the leakage resistance, form and maintain the closed sealing ring required for sealing, reduce the influence of the medium pressure difference and concentration difference, and stabilize the sealing performance. Therefore, it should be based on the working pressure of the valve. The height and diameter increase or decrease. Since the sealing force and correcting force will also increase or decrease synchronously, it is necessary to balance and adjust the width of the sealing surface according to the limit of the closing torque.

(3) Thickness L of sealing layer

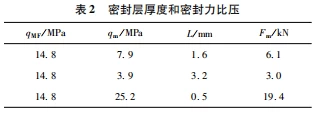
It can be observed in the sealing test that the sealing layer is thicker than thinner. Taking the H44W-64P-DN50 valve as an example, bm=45 mm, E=21×105 MPa, a=03 μm, ε=024 μm, when the thickness of the sealing layer increases from 16 mm When it reaches 32 mm, the specific pressure of the sealing force drops by 50% (Table 2), which drives the sealing force to decrease year-on-year and improves the matching process of the sealing pair. On the contrary, if the sealing layer is thinned, the sealing force needs to be increased, which increases the difficulty of pairing. In the process of elastic deformation, the thickness of the sealing layer should be inversely proportional to the compressive stress, but in the example, the increase or decrease of the thickness of the sealing layer did not change the calculated value of the necessary specific pressure.

Table 2 Seal thickness and sealing force specific pressure

(4) Surface roughness of sealing surface

The process of obtaining the sealing compressive stress on the metal sealing surface is essentially the process of changing the surface roughness, but this process must not be shown in the specific pressure calculation mode. Therefore, the change of the surface roughness before and after the extrusion of the sealing surface does not and cannot change the calculated value of the necessary specific pressure, so that, like the thickness of the sealing layer, the basis for process regulation and quality control is lost.

(5) Elastic modulus E

The elastic moduli of brass and bronze are not equal, and the material constant C in the calculation formula adopts a uniform fixed value of 30, which covers the difference of material properties among various grades with an error of plus or minus 20%. If the sealing surface is changed from brass to stainless steel, only the constant C is changed from 30 to 35 in the calculation formula of the necessary specific pressure, and the qMF is only increased by 14%~4%. According to Hooke's law, qm will double as the elastic modulus changes.

(6) Rubber compression rate δ

Taking D371X-16Q-DN300 valve as an example, set D0=300 mm, E=784 MPa, L=55 mm, DM=3018 mm, r=5 mm, then the rubber compression rate δ=165 mm 4%, the sealing force specific pressure qm=13 MPa. At this time, the effective projected width of the sealing surface bm=394 mm (the chord length of the compression ratio is more than 9%), then its specific pressure qMF=22 MPa, but it has nothing to do with the compression ratio, and the specific sealing force is proportional to the pressure 70% larger. This error will be brought into subsequent calculations of part strength and so on.

4.3 Analysis of sealing force specific pressure

The analysis shows that the calculated value of the necessary specific pressure does not accurately meet the necessary conditions for sealing, and the sealing performance cannot be changed by adjusting the relevant parameters of the sealing. Since the specific pressure of the sealing force is not included in the specific pressure of the corrective force, its value is the same as the calculated value of the necessary specific pressure.

5. Correction force ratio

Grinding the metal sealing surface such as hard face for high temperature application pressure seal gate valve can reduce the surface shape error of the machined plane, but it is impossible to eliminate the error, especially the sealing surface placed in the valve body cavity, and the flatness error brought by the grinding tool to the sealing surface. If the width of the two sealing surfaces is inconsistent, the flatness of the wider sealing surface needs to be converted into the flatness error value for the calculation according to the area of the narrower sealing surface. Different processing methods make the surface flatness have different directionality, so it is necessary to calculate the gap between the two sealing surfaces according to the assembly form of the two surface flatness in the same direction or opposite or even disordered. Eliminating the gap needs to rely on the total force on the sealing surface to squeeze the surface roughness peak of the sealing surface, or to press the valve disc base to bend and deform.

5.1 Correction force specific pressure calculation formula

(1) Squeeze the sealing surface

The total extrusion rate of the peaks of the sealing surface cannot exceed 50 % of the surface roughness of the sealing surface after grinding. In the example of solving the material coefficients C and K in the calculation formula of the necessary specific pressure, it can be seen that the extrusion rate λ of the wave crest of the metal sealing surface required to obtain the sealing force generally does not exceed 30%, so the correction force is only reserved for not only to 20%a. This kind of small gap occurs only when the surfaces of the two sealing surfaces in the sealing pair are inclined in the same direction. Let the minimum distance ω between the sealing pairs be the difference between the two flatness error values, when ω≈(10 %~20 %) a When , the correction force specific pressure qh≈(02~04)qm.

(2) Matrix deformation

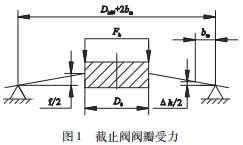
In most cases, ε exceeds 15 % a, which can only reduce the flatness error by compressing the bending deformation of the valve disc base. Taking the globe valve as an example, if the two sealing surfaces of the sealing pair are inclined toward each other, the gap opening faces inward and connects with the valve seat flow channel, and the rigidity of the disc base is less than that of the valve body interlayer. The base of the valve disc is a circular plate, the intersection of the head of the valve disc and the base body is the inner edge, and the outer diameter of the sealing surface of the valve seat is the outer edge. The torus plate produces deflection f (Fig. 1). The correction force Fh is calculated according to the circular plate formula of concentrated load [3]。

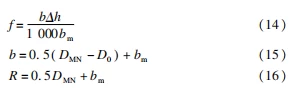
in the formula

f——the deflection of the annular plate, mm

b——the annular width of the annular plate, mm

β——The calculation coefficient of the deflection of the annular plate (check the calculation coefficient of the deflection of the annular plate according to the r/R ratio [3])

R——Radius of annular plate (outer radius of valve seat), mm

r——radius of annular hole (outer radius of disc head, r=05D0), mm

According to the definition of compressive stress, the specific pressure qh of the corrective force on the sealing surface is

5.2 Correction force specific pressure analysis

If the two sealing surfaces of the sealing pair of the globe valve are inclined towards each other and the gap opening faces outward, the larger opening will only increase the gap after the valve disc is bent and deformed under pressure. Therefore, only by controlling the cutting feed direction to change the tilt direction of the surface flatness, this type of assembly can be avoided. Different valve structures and the shape error of the sealing surface affect the clear choice of the mechanical model and calculation mode. However, most of them are realized by the bending deformation of the valve disc base, and the maximum value of the correction force is representative. The selection of the calculation formula of the annular plate should be based on the load properties of the valve disc. For example, the check valve is a uniform load, and the calculation procedures are also very different. Since the thickness of the disc base appears as a power of 3 in the calculation formula of the circular plate, as long as there is a slight increase or decrease, the qh value will be quickly pulled. If the thickness is out of control (such as setting an excessive thickness additional allowance), it is very likely that the closing torque will exceed the limit, or the actual contact width of the sealing surface will be narrowed because the flatness error of the sealing surface cannot be completely eliminated, thereby reducing the service life of the valve and Sealing reliability (these are not suitable for discs below DN65 without or with a narrow annular flat base).

6. Sealing pressure ratio

6.1 Calculation formula of sealing specific pressure

The analysis shows that the valve sealing has to go through two processes. First, the shape error of the sealing surface (spherical, conical or flat) is eliminated by the corrective force, and a contact surface with sufficient width is obtained, and then the contact surface is squeezed by the sealing force to form an effective seal. sealing ring. Therefore, the sealing force FMB is

6.2 Analysis of sealing specific pressure

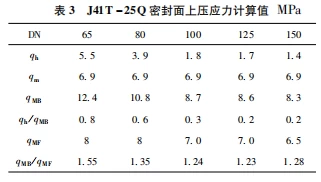
Table 3 lists the calculated values and ratios of various compressive stresses on the J41T-25Q-DN65~DN150 sealing surface (the thickness of the substrate is calculated according to the strength). The force specific pressure is 20%~80% of the sealing specific pressure value. Although there are particularities in individual cases, small changes in seal-related parameters can have a large impact on the calculation results. For example, increasing the thickness of the sealing layer from 15 mm to 2 mm will reduce the proportion of the sealing specific pressure exceeding the necessary specific pressure by about 25%, that is, qMB≈(10~13) qMF. But at least it can be seen that the value of the corrective force is not negligible. It is more difficult and more important to control and reduce the shape error of the sealing surface than the surface roughness. It reveals the distribution of the force in the sealing force, and the process direction to achieve and improve the sealing. . Therefore, it is necessary to put forward clear requirements on the shape error level of the sealing surface in the selection of design parameters, as with the surface roughness.

(1) Calculation formula of metal seal specific pressure

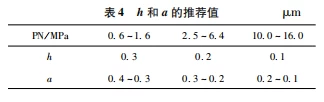
Adjust and control the thickness of the sealing layer by the calculation formula of sealing force and pressure. The general value range is recommended as (calculated at the thinnest point, excluding the metal transition layer of surfacing welding) L≥20 mm, copper alloy L≥2 15 mm. The recommended values of surface roughness a and sealing surface flatness h after grinding are shown in Table 4. Since the check valve has no external sealing force to use, it should be improved by at least one level, and for materials such as copper alloys with lower hardness and small elastic modulus, the roughness of the sealing surface can be relaxed by one level. For example, PN16, the surface roughness a can be relaxed to Ra08 μm. According to the statistical tracking of measurement data, Ra02~04 μm can be achieved by conventional grinding process, but 01 μm needs to be precisely ground.

(2) Calculation formula of rubber seal specific pressure

The compression ratio of the medium-hardness rubber sealing surface can be sealed within 8%≤δ≤33%, but if the compression ratio is controlled to δ=15%~25%, the sealing performance is relatively stable. Permanent loss of sealing capability is possible. The elastic modulus of medium hardness rubber (referring to 75 A±5 A) is E=784 MPa, and the elastic modulus of rubber with a hardness of 60~70 A will decrease, which is taken according to SL74-2013. The thickness L of the rubber layer should be calculated and determined according to the control ability of the dimensional deviation of the sealing pair to ensure that the actual compression rate δ of the rubber sealing layer is always controlled within a reasonable range when the metal seal is in the maximum solid and the minimum solid. When the thickness is too thin, its compressibility is unstable and its strength is not enough, generally L≥2 mm.

(3) Calculation formula of specific pressure of PTFE seal

The compressive elastic modulus of PTFE is generally E=280 MPa, but it should be adjusted according to the actual measured value of the selected material. The compressibility of the flat seal is limited by the compressive strength at different operating temperatures. For the ball valve seat that is pressurized on both sides in a fixed space, it is also subject to the cold flow resistance (false yield limit). The compression ratio δ is calculated according to formula (8), which is superimposed by the compression ratio of the static sealing surface and the dynamic sealing surface.

8. Conclusion

(1) In the calculation formula of the necessary specific pressure, the constant term C and coefficient K related to the material of the sealing surface cannot show the influence of the change of the elastic modulus, the thickness of the sealing surface and the roughness of the sealing surface on the necessary specific pressure, and there is no The corrective force specific pressure is included, so the necessary specific pressure calculation formula for metal seals is limited. When the formula for calculating the necessary specific pressure for non-metallic seals is used, the calculation result is not practical because it cannot be correlated with the compressibility.

(2) Hooke's law can be used to interpret and copy the calculation formula of the necessary specific pressure, and deduce the calculation formula of the specific pressure of the correction force and the specific pressure of the sealing force.

(3) The specific pressure of the sealing force is proportional to the elastic modulus of the metal sealing surface material and the difference (compression) of the surface roughness before and after extrusion, inversely proportional to the thickness of the sealing layer, and has nothing to do with the width of the sealing surface.

(4) The width of the sealing surface is related to the mechanical strength and service life of the sealing layer. A wider sealing surface is conducive to the formation of a closed sealing ring, reducing the influence of the medium pressure difference or concentration difference, and stabilizing the sealing performance. Therefore, it should be based on the work of the valve. Limit setting of pressure level, caliber size and closing torque.

(5) The sealing specific pressure is composed of the sealing force specific pressure and the correction force specific pressure

Symbol Description:

C, K - coefficients related to the material of the sealing surface

a——The surface roughness of the sealing surface after grinding, μm

DMN - the inner diameter of the valve seat,

mm ε——The surface roughness of the sealing surface after extrusion, μm

Do—— Disc head diameter, mm

λ——Seal surface crest extrusion rate, %

A—— area of ​​sealing surface, mm2

ΔL——The peak height of the flattened surface of the sealing surface, μm

ω——The difference between the flatness error values ​​of the two sealing surfaces of the sealing pair, μm

L——The thickness of the sealing layer, mm

Δh——the sum of the flatness errors of the two sealing surfaces of the sealing pair, μm

δ——compression rate of sealing layer, %

h——flatness of the sealing surface after grinding, μm

p—— medium working pressure, MPa

bm——the width of the sealing surface of the plane seal, mm

PN - Nominal pressure, MPa

q——The calculated specific pressure of the sealing surface (actual specific pressure), MPa

FMZ——Total force on the sealing surface, N

qMB——seal specific pressure, MPa

FMB - sealing force, N

qm——The specific pressure of sealing force, MPa

Fm - sealing force, N

qh——correction force specific pressure, MPa

Fh——correction force, N

qMF——must be specific pressure, MPa

DM—— Outer diameter of disc, mm

[q]——Allowable specific pressure, MPa

r—— the sealing arc radius of the disc edge, mm

E - elastic modulus of the material, MPa

t——the thickness of the base of the valve disc, mm